Δεν υπάρχουν ασήμαντοι αριθμοί.
Απόδειξη
Αν υπήρχαν κάποιοι ασήμαντοι αριθμοί, τότε ένας από αυτούς θα ήταν ο μικρότερος. Αυτό όμως είναι αδύνατο, γιατί αυτός ο αριθμός θα ήταν "ο μικρότερος ασήμαντος αριθμός", πράγμα που τον κάνει σημαντικό, άρα δεν μπορεί να ανήκει στο σύνολο των ασήμαντων.
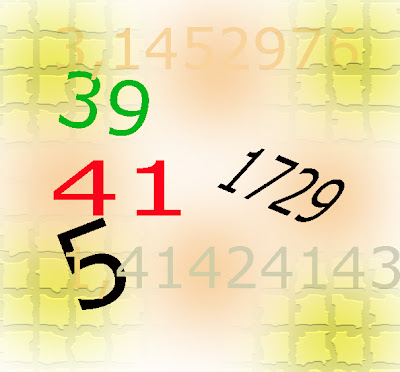
Ας δούμε όμως μια άλλη θεώρηση, που θα μας "αποδείξει" ότι ο 41 είναι ασήμαντος.
Κάνουμε την υπόθεση ότι ο 39 και ο 41 είναι οι πρώτοι ασήμαντοι αριθμοί.
Ομως ο 39 είναι ο μικρότερος από τους δύο, άρα είναι σημαντικός, γιατί είναι ο μικρότερος ασήμαντος, άρα δεν μπορεί να ανήκει στο σύνολο των ασήμαντων, άρα η λύση στο ερώτημά μας είναι ο 41.
Μια φορά ο Αγγλος μαθηματικός G. H Hardy πήγαινε στο νοσοκομείο να δει τον Ινδό μαθηματικό Srinivasa Ramanujan. Το ταξί που τον μετέφερε είχε αριθμό 1729 και ο Hardy σκέφτηκε ότι είναι ένας ασήμαντος αριθμός, το οποίο είπε στον Ramanujan. Εκείνος πετάχτηκε από το κρεββάτι του και του είπε "Τι είναι αυτά που λες, ο 1729 είναι ο μικρότερος αριθμός που εκφράζεται σαν άθροισμα δύο κύβων με δύο διαφορετικούς τρόπους !!"
Πράγματι,
Απόδειξη
Αν υπήρχαν κάποιοι ασήμαντοι αριθμοί, τότε ένας από αυτούς θα ήταν ο μικρότερος. Αυτό όμως είναι αδύνατο, γιατί αυτός ο αριθμός θα ήταν "ο μικρότερος ασήμαντος αριθμός", πράγμα που τον κάνει σημαντικό, άρα δεν μπορεί να ανήκει στο σύνολο των ασήμαντων.
Κάνουμε την υπόθεση ότι ο 39 και ο 41 είναι οι πρώτοι ασήμαντοι αριθμοί.
Ομως ο 39 είναι ο μικρότερος από τους δύο, άρα είναι σημαντικός, γιατί είναι ο μικρότερος ασήμαντος, άρα δεν μπορεί να ανήκει στο σύνολο των ασήμαντων, άρα η λύση στο ερώτημά μας είναι ο 41.
Μια φορά ο Αγγλος μαθηματικός G. H Hardy πήγαινε στο νοσοκομείο να δει τον Ινδό μαθηματικό Srinivasa Ramanujan. Το ταξί που τον μετέφερε είχε αριθμό 1729 και ο Hardy σκέφτηκε ότι είναι ένας ασήμαντος αριθμός, το οποίο είπε στον Ramanujan. Εκείνος πετάχτηκε από το κρεββάτι του και του είπε "Τι είναι αυτά που λες, ο 1729 είναι ο μικρότερος αριθμός που εκφράζεται σαν άθροισμα δύο κύβων με δύο διαφορετικούς τρόπους !!"
Πράγματι,
- 1729 = 13 + 123 = 93 + 103
Nαι, αλλά ,μέρα πού'ναι..(γενέθλια του Ντάγκλας Άνταμς), ο σημαντικότερος από τους σημαντικούς αριθμούς είναι σίγουρα το 42, πράγμα που κάνει το 41 τον προηγούμενο του σημαντικότερου ,άρα εξίσου σημαντικό...κλπ,κλπ... :-)
ΑπάντησηΔιαγραφήNα γράφεις συχνότερα αγαπητέ! Μας έλειψες!
Kύριε Τσοκάκη, μία ερώτηση:
ΑπάντησηΔιαγραφήΈχω την άδειά σας να αναπαραγάγω το κείμενό σας (με αναφορά φυσικά στο όνομά σας και στο μπλογκ)σε άλλο ιστολόγιο (μαθηματικού περιεχομένου);
Εξυπακούεται, ότι και σε περίπτωση άρνησης ,πάλι αδέρφια θάμαστε!:-)
Η αναπαραγωγή είναι ελεύθερη και επιθυμητή !!
ΑπάντησηΔιαγραφή