Οταν ο βασιληάς Μίνωας είδε τον κυβικό τάφο του γιου του Γλαύκου, του φάνηκε μικρός και έδωσε διαταγή να τον διπλασιάσουνε.
Μια άλλη φορά, ο θεός Απόλλωνας έρριξε λοιμό στη Δήλο και οι κάτοικοι ρώτησαν το μαντείο των Δελφών τι να κάνουν. "Να διπλασιάσετε τον όγκο του κυβικού βωμού του θεού"
Με τον ένα ή με τον άλλο θρύλο, προέκυψε ένα από τα διάσημα προβλήματα της αρχαιότητας, πώς φτιάχνουμε ένα κύβο διπλάσιου όγκου από τον αρχικό.
Επειδή η ακμή αυτού του κύβου είναι η κυβική ρίζα του 2, αριθμός ασύμετρος, η κατασκευή δεν γίνεται με κανόνα και διαβήτη, άρα πρέπει να αναζητηθούν άλλες μέθοδοι.
Ο Πλάτωνας, απ' ότι μας λέει ο Πλούταρχος, έδωσε το πρόβλημα στους μαθητές του, μερικοί από αυτούς, όπως ο Εύδοξος και ο Μέναιχμος, το έλυσαν, αλλά του Πλάτωνα δεν του άρεσε που οι μαθητές του χρησιμοποιούσαν "μοντέρνους" τρόπους και ξέφευγαν από τα παραδοσιακά !!
Εκατό χρόνια πριν ο Ιπποκράτης ο Χίος [470-410 πΧ] είχε μιλήσει για τον διπλό μέσο ανάλογο. Ανάμεσα σε δύο αριθμούς α και β υπάρχουν οι χ και ψ έτσι ώστε
Μια άλλη φορά, ο θεός Απόλλωνας έρριξε λοιμό στη Δήλο και οι κάτοικοι ρώτησαν το μαντείο των Δελφών τι να κάνουν. "Να διπλασιάσετε τον όγκο του κυβικού βωμού του θεού"
Με τον ένα ή με τον άλλο θρύλο, προέκυψε ένα από τα διάσημα προβλήματα της αρχαιότητας, πώς φτιάχνουμε ένα κύβο διπλάσιου όγκου από τον αρχικό.
Επειδή η ακμή αυτού του κύβου είναι η κυβική ρίζα του 2, αριθμός ασύμετρος, η κατασκευή δεν γίνεται με κανόνα και διαβήτη, άρα πρέπει να αναζητηθούν άλλες μέθοδοι.
Ο Πλάτωνας, απ' ότι μας λέει ο Πλούταρχος, έδωσε το πρόβλημα στους μαθητές του, μερικοί από αυτούς, όπως ο Εύδοξος και ο Μέναιχμος, το έλυσαν, αλλά του Πλάτωνα δεν του άρεσε που οι μαθητές του χρησιμοποιούσαν "μοντέρνους" τρόπους και ξέφευγαν από τα παραδοσιακά !!
Εκατό χρόνια πριν ο Ιπποκράτης ο Χίος [470-410 πΧ] είχε μιλήσει για τον διπλό μέσο ανάλογο. Ανάμεσα σε δύο αριθμούς α και β υπάρχουν οι χ και ψ έτσι ώστε
α/χ = χ/ψ = ψ/β (1)
Αν λοιπόν β=2α, τότε θα υπάρχουν οι αριθμοί r και s έτσι ώστεα/r = r/s = s/2α (2)
οπότε η ζητούμενη πλευρά είναι η r
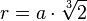
O Μέναιχμος [380-320 πΧ]
παρουσίασε δύο λύσεις, στηριγμένος στην παρατήρηση του Ιπποκράτη και ανοίγοντας το σπουδαίο κεφάλαιο των κωνικών τομών.
Αν στην σχέση (1) βάλουμε α=1 και β=2 έχουμε
1/χ = χ/ψ = ψ/2
από όπου προκύπτουν οι σχέσεις
ψ2 = 2χ και ψ = χ2
Αυτές οι σχέσεις είναι δύο κωνικές τομές και η λύση βρίσκεται ακριβώς στην τομή τους.
Ετσι λοιπόν ο Μέναιχμος συνδέει οριστικά το πρόβλημα διπλασιασμού του κύβου με τις τριάδες του Ιπποκράτη του Χίου και τις κωνικές τομές, ανοίγοντας τον δρόμο για τον Απολλώνιο, τον Αρχιμήδη και τη γέννηση της αναλυτικής γεωμετρίας τον μεσαίωνα.
Ηταν τόσο οριστική και για τον αρχαίο κόσμο η σύνδεση, ώστε να βλέπουμε στις περισσότερες μεταγενέστερες αναφορές τον Μέναιχμο και τις τριάδες του.
[Πρόκλος, Ὑπόμνημα εἰς τὸ πρώτον τῶν Εὐκλείδου Στοιχείων, 4ος αι. μΧ].
Αυτές οι εξαιρετικές επινοήσεις των Ελλήνων μαθηματικών ταξίδεψαν σε όλο τον κόσμο και, χάρη στις μεταφράσεις των Αράβων έγιναν για δεύτερη φορά γνωστές στη μεσαιωνική δύση και αποτέλεσαν την αφετηρία της αναγέννησης.
Ο Μέναιχμος υπήρξε δάσκαλος του Μεγαλέξαντρου.
Μια φορά λοιπόν, ο βιαστικός νεαρός βασιληάς ζήτησε από τον Μέναιχμο να του διδάξει στα γρήγορα την επιστήμη της Γεωμετρίας.
"Στη χώρα μας, βασιληά μου, υπάρχουνε ιδιωτικοί και βασιλικοί δρόμοι. Ο δρόμος της Γεωμετρίας όμως είναι ένας και είναι ίδιος για όλους"
απάντησε ο Μέναιχμος, παρακάμπτοντας την αξίωση του απόλυτου στρατηλάτη.
[Ιωάννου Στοβαίου, Ανθολόγιον]








